Résumé cours : dérivabilité
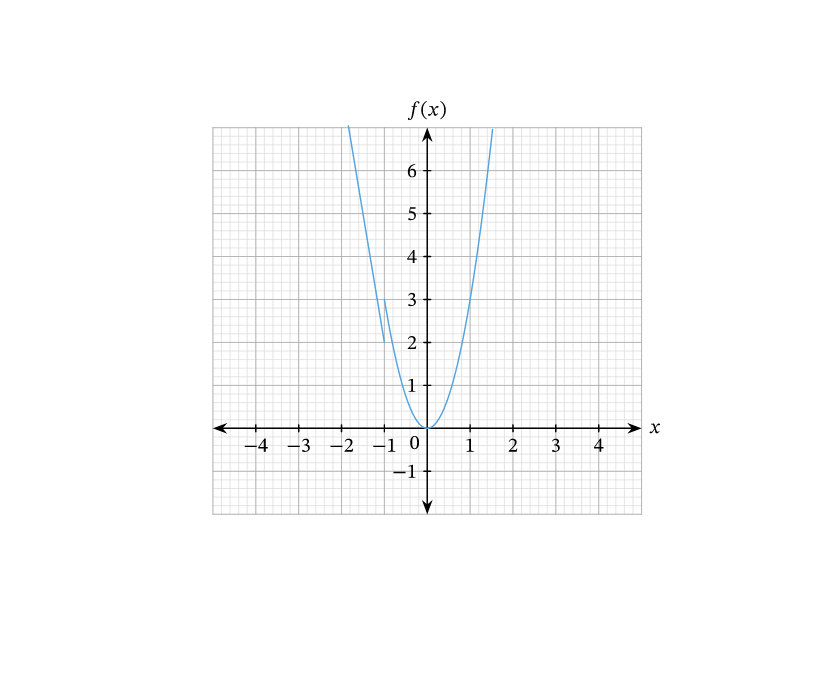
Une fonction réelle d'une variable réelle est dérivable en un point a quand elle admet une dérivée finie en a, c'est-à-dire, intuitivement, quand elle peut être approchée de manière assez fine par une fonction affine au voisinage de a.
f est une fonction dérivable en tout point x d’un intervalle I inclus dans son domaine de définition.
La fonction qui à tout réel x de I associe f′(x), le nombre dérivé de f en x, est la fonction dérivée de f sur I. On la note f‘.
Vous pouvez télécharger le résumé complet des théorèmes et des fonctions usuelles sur les dérivés.
Catégories
Savoirs les plus récents
-
Création de tableaux en HTML
HTML5 -
PHP DateTime : créez, comparez et formatez des dates
PHP -
Correction algorithme : Généalogie
Algorithmes -
Correction algorithme : Coupe du monde
Algorithmes -
Correction algorithme : Découpage et collage
Algorithmes

